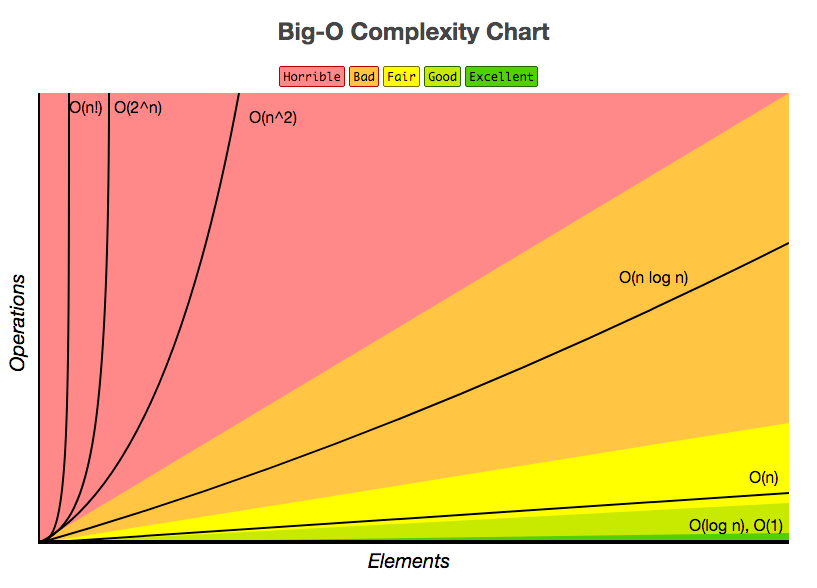
Big O notation, in short, describes two things:
- The rate of increase of an algorithm’s runtime with respect to its input
- The amount of memory space required to process the input
All algorithms have a worst case, average case and a best case scenario.
bigocheatsheet.com
Constant Time // O(1) or O(c)
The algorithm takes a constant time to process, no matter the amount of data in the set.
Examples:
- Retrieve the nth element in an array
- Insert an element into a hash table (assuming no collisions)
- Delete an element in a hash table
Linear Time // O(n)
The algorithm takes an amount of time, linear with the size of the set and is proportional to the number of items in the collection.
Examples:
- Find a specified element in an array
- Delete a specified element in an array
- Find x element in a stack
- Print out all of the elements in a list
Logarithmic Time // O(log n)
An attribute of a logarithmic running-time algorithm is that the choice of the next element on which to perform an action is one of several possibilities — only one will need to be chosen. To best illustrate this algorithm, imagine you’re looking for a name in the phonebook. You won’t have to check every single name. You’ll likely divide the phonebook and search the half which the name is likely to be alphabetically, and keep doing so until you find the name.
In this way, while larger inputs do take longer, it won’t increase as quickly as the proportional increase in the additional size.
Examples:
- Binary search tree
- Skip list
- Find a specific element in a sorted collection
Polynomial Time // O(n²)
This represents an algorithm whose performance is directly proportional to the square of the size of the input data set. This is common with algorithms that involve nested iterations over the data set (with deeper nested iterations resulting in O(n³) or O(n⁴)).
Examples:
- Compare each element in an array to all the other elements in the array
- Check if a list contains duplicates
Exponential Time // O(2^n)
This denotes an algorithm whose growth doubles with each addition to the input dataset.
Examples:
- Fibonacci recursive solution
Additional Big O Complexities:
- Linearithmic — n log(n)
- Log squared — log(n²)
- Cubic — O(n³)
- Factorial — O(n!)



